=
=
 - h,
- h, Methods Background: Topological Indices
This chapter presents brief background information on some of the indices computed by Molconn-Z. The user is referred to the materials cited below for more detailed information.
Definition: Molecular connectivity is a method of molecular structure quantitation in which weighted counts of substructure fragments are incorporated into numerical indices. Structural features such as size, branching, unsaturation, heteroatom content and cyclicity are encoded.
 =
=
 - h,
- h,
where  is the count of electrons in
is the count of electrons in
 orbitals and h is the count of
hydrogen atoms. This simple
orbitals and h is the count of
hydrogen atoms. This simple  value of an atom is equal to the
number of neighboring atoms in the molecular skeleton. The
value of an atom is equal to the
number of neighboring atoms in the molecular skeleton. The  values of each atom are subsequently used in calculating the simple
molecular connectivity indices. The valence electron descriptor is
given as
values of each atom are subsequently used in calculating the simple
molecular connectivity indices. The valence electron descriptor is
given as
 v = Zv - h,
v = Zv - h,
where Zv is the count of the valence electrons.
A more general expression for  v which includes atoms in the 2nd, 3rd,
and 4th rows of the periodic chart is
v which includes atoms in the 2nd, 3rd,
and 4th rows of the periodic chart is
 v = (Zv - h)/(Z - Zv -1),
v = (Zv - h)/(Z - Zv -1),
where Z is the count of all electrons, the atomic number. The valence delta values are used in calculating the valence molecular connectivity indices.
The molecular connectivity indices or chi indices are symbolized
m t.
Substructures for a molecular skeleton are defined by the decomposition
of the skeleton into fragments of:
t.
Substructures for a molecular skeleton are defined by the decomposition
of the skeleton into fragments of:
a) atoms (zero order, m = 0);
b) one bond paths (first order, m = l);
c) two bond fragments (second order, m = 2);
d) three contiguous bond fragments (third order Path, m = 3, t = P);
and so forth. Other fragments include the cluster
(three atoms attached to a central atom, m = 3, t = C);
the path/cluster (equivalent to the isopentane skeleton, m = 4, t = PC);
the chain fragment (cycles of 3, 4, 5 . . . atoms, m = 3, 4, 5. . ., t = CH).
For each order and fragment type, a connectivity index may be calculated.
This calculation is made by multiplying the  (or
(or  v) values for each
atom in a fragment within a molecule. This product is then converted
to the reciprocal square root and called the connectivity subgraph
term ci. These terms are then summed over all the subgraphs
(of order m and type t) in the entire molecule, Ns, to calculate
the molecular connectivity index
m
v) values for each
atom in a fragment within a molecule. This product is then converted
to the reciprocal square root and called the connectivity subgraph
term ci. These terms are then summed over all the subgraphs
(of order m and type t) in the entire molecule, Ns, to calculate
the molecular connectivity index
m t
of order m and type t.
t
of order m and type t.
m+1 Ns mci =The valence molecular connectivity indices m(
k)-0.5 and m
t =
mci k=1 i=1
 tv
are calculated in the
same way using
tv
are calculated in the
same way using  v values throughout.
v values throughout.The calculations are made from input information which includes the connection matrix, designation of the atom type, and the count of bonded hydrogens to each atom. The valence delta values are determined in the program from the formalism given above.
| Structural Formula | |
 | |
| Hydrogen-suppressed Graph or Molecular Skeleton | |
To calculate 1 v, dissect the molecule into all its one-bond fragments,
shown below; each bond fragment is labeled with the
v, dissect the molecule into all its one-bond fragments,
shown below; each bond fragment is labeled with the
 v values.
v values.
For each fragment compute the subgraph contribution,
(vi *
vj )-0.5,
and sum over all the bond fragments:
1v = 3.6175.
In an analogous manner the other connectivity indices can be calculated for
path, cluster, path/cluster and ring type subgraphs. The finding of
all the subgraphs of a given type becomes a difficult computational
problem by hand. That is, of course, the reason for the development
of Molconn-Z.
Definition: The Kappa shape indices are the basis of a method of
molecular structure quantitation in which attributes of molecular
shape are encoded into three indices (Kappa values). These
Kappa values are derived from counts of one-bond, two-bond and
three-bond fragments, each count being made relative to fragment
counts in reference structures which possess a maximum and minimum
value for that number of atoms.
Below are the graphs for the structures corresponding to the maximum count
of paths for orders 1, 2, and 3 in 6-atom molecules.
Molecular Shape Indices
References
The Method
The calculation of the indices begins with the reduction of the molecule to
the hydrogen-suppressed skeleton. The count of 1-, 2-, and 3-bond fragments,
1P, 2P and 3P, respectively, is made. These values are used in calculating
the Kappa indices 1 , 2
, 2 , and
3
, and
3 . The calculation of each index is made
using the value of mPi and the mPmin and mPmax
counts for graphs with the
same number of atoms, A. These latter counts are the minimum and maximum
numbers of paths of that order (m) that can be found in a real or
hypothetical structure. Specifically, the mPmin for all orders of
Kappa is the count of paths of length m in the linear skeleton.
The mPmax structure is, for the m = 1, a complete graph (a);
for m = 2, a star graph (b); and for m = 3, a twin star graph (c).
. The calculation of each index is made
using the value of mPi and the mPmin and mPmax
counts for graphs with the
same number of atoms, A. These latter counts are the minimum and maximum
numbers of paths of that order (m) that can be found in a real or
hypothetical structure. Specifically, the mPmin for all orders of
Kappa is the count of paths of length m in the linear skeleton.
The mPmax structure is, for the m = 1, a complete graph (a);
for m = 2, a star graph (b); and for m = 3, a twin star graph (c).
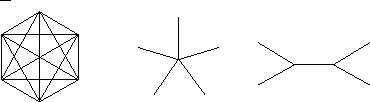
(a) (b) (c)
 = A(A-l)2/(1Pi)2
= A(A-l)2/(1Pi)2
 = (A-1)(A-2)2/(2Pi)2
= (A-1)(A-2)2/(2Pi)2
 = (A-3)(A-2)2/(3Pi)2; A is even
= (A-3)(A-2)2/(3Pi)2; A is even
 = (A-1)(A-3)2/(3Pi)2; A is odd
= (A-1)(A-3)2/(3Pi)2; A is oddThe presence of atoms other than C(sp3) is taken into consideration in each order of Kappa index by modifying each A and mPi in the equations above with a value:
where r(x) is the covalent radius of atom x and r[C(sp3)] is the covalent radius of carbon in the sp3 hybrid state. In the relation for the Kappa indices, A is replaced by A += r(x)/r[C(sp3)] - 1
 and mPi is replaced by mPi +
and mPi is replaced by mPi +  .
The resulting Kappa values are designated as m
.
The resulting Kappa values are designated as m
 . See
Appendix II
for the set of values currently used in the kappa shape indices.
. See
Appendix II
for the set of values currently used in the kappa shape indices.
In some small molecules, certain of the mP quantities may not be
defined or are considered to be zero. This presents problems in
applying the kappa algorithm. We consider one approach to solving
this problem. The calculation of a 1 value is possible for any
molecule except those represented by a single point, i.e., methane.
In this case, 1
value is possible for any
molecule except those represented by a single point, i.e., methane.
In this case, 1 = 0 from the general equation for kappa-1.
In general, for a straight chain molecule, 1
= 0 from the general equation for kappa-1.
In general, for a straight chain molecule, 1 = A, and so an
extrapolated value of 1
= A, and so an
extrapolated value of 1 = 1.000 is adopted for methane.
= 1.000 is adopted for methane.
The calculation of 2 values leads to non-zero values in all cases
except for any graph representation of one or two atoms, such as
methane and ethane. In both cases, 2
values leads to non-zero values in all cases
except for any graph representation of one or two atoms, such as
methane and ethane. In both cases, 2 from the general equation
is zero. In general, for straight chain molecules, 2
from the general equation
is zero. In general, for straight chain molecules, 2 = A - 1.
Values of 2
= A - 1.
Values of 2 = 1.000 for ethane and
2
= 1.000 for ethane and
2 = 0 for methane are extrapolated and proposed as useful in
cases where these molecules are part of a structure-activity analysis.
= 0 for methane are extrapolated and proposed as useful in
cases where these molecules are part of a structure-activity analysis.
In the case of 3 values calculated from the general equations,
the values for methane, ethane, and propane, are zero while the value for butane is 4.000,
the same as for pentane. By linear extrapolation, more useful 3
values calculated from the general equations,
the values for methane, ethane, and propane, are zero while the value for butane is 4.000,
the same as for pentane. By linear extrapolation, more useful 3 values for these molecules are derived: methane 3
values for these molecules are derived: methane 3 = 0, ethane
3
= 0, ethane
3 = 1.450, propane 3
= 1.450, propane 3 = 2.000, and butane 3
= 2.000, and butane 3 = 3.378. These estimates are used to
provide numerical values for small molecule which may appear in a series.
= 3.378. These estimates are used to
provide numerical values for small molecule which may appear in a series.
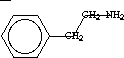
 [C(sp3)] = -0.13; total
[C(sp3)] = -0.13; total  = -0.82
= -0.82 [NH2] = -0.04
[NH2] = -0.04

 = (A +
= (A +  - 1)(A +
- 1)(A +  - 2)2/(2Pi +
- 2)2/(2Pi +  )2
)2

 = 3.254
= 3.254
Each atom in the skeleton structure of a molecule is identified by the valence
delta values described above. Beginning with any atom i, all contiguous paths
of atoms, emanating from that atom to each other atom j, are identified. The
lowest order path is the atom itself. This process is followed by finding all
first order paths (bonds containing atom i) and so on ultimately including the
longest paths(s) terminating on atom i. A numerical value is calculated for
each of these paths and is an entry in the Topological State Matrix T. Each
entry is calculated according to the formula
Topological State Indices
Definition: The topological state indices are numerical values associated
with each atom in a molecule and which encode information about the
topological environment of that atom due to all other atoms in the
molecule. The topological relationship to each other atom is based
on the encoding of atom information in all the paths emanating from
that atom. Topologically equivalent atoms have identical values
of the topological state index Si and inequivalent atoms have
different values.References
The Method
tij = (GMij)a(dij)b.GMij is the geometric mean of the delta values of the atoms in the path of atoms of length dij atoms between atoms i and j. These path fragment values are then summed to give a topological state value Ti for atom i. Subsequent calculations produce Ti values for every atom. Several values of a and b have been investigated. Note: In reference 1 the symbol used for topological state was Si rather than Ti which is the proper symbol. We have adopted the symbol Si for the electrotopological state index, described in the next section.
The default option value <4> for the Topological State Algorithm in the Molconn-Z program uses a = +1 and b = -2:
tij = (GMij)a(dij)b.
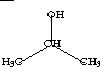
| Topological State Index, Ti | |||||||||
| 1 | CH3- | CH3CH- | CH3CHCH3 | CH3CHOH | 1.000 | 1.154 | 2.080 | 1.216 | |
| 2 | -CH< | >CHCH3 | >CHOH | 1.154 | 0.333 | 1.154 | 0.516 | ||
| 3 | CH3 | CH3CHOH | 2.080 | 1.154 | 1.000 | 1.216 | |||
| 4 | -OH | 1.216 | 0.516 | 1.216 | 0.200 | ||||
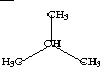
| Topological State Index, Ti | |||||||||
| 1 | CH3- | CH3CH- | CH3CHCH3 | CH3CHCH3 | 1.000 | 1.154 | 2.080 | 2.080 | |
| 2 | -CH< | >CHCH3 | >CHCH3 | 1.154 | 0.333 | 1.154 | 1.514 | ||
| 3 | CH3 | CH3CHCH3 | 2.080 | 1.154 | 1.000 | 2.080 | |||
| 4 | -CH3 | 2.080 | 1.154 | 2.080 | 1.000 | ||||
In these examples it can be observed that topological equivalence is indicated by the Ti values. In 2-propanol the topological equivalence of the two methyl groups is shown by the fact that T1 = T3; no other values are equal in accordance with the fact that no other atoms are topologically equivalent. In isobutane, three Ti values are equal, T1 = T3 = T4, in keeping with the fact that the three methyl groups are equivalent and the central methine group is unique. In this sense, the topological state index values represent the topological equivalence (topological symmetry) of the molecule. The pattern of Ti values for a portion of a molecule appears to be characteristic of that fragment and may be used as a basis for quantitative measures of fragment similarity.
Ii = [(2/N)2  v + 1]/
v + 1]/
The intrinsic state encodes the
valence state electronegativity of the atom as well as its local topology through the use of the molecular
connectivity simple and valence delta values,  and
and  v.
v.
The perturbation on atom i, arising from the presence of all other atoms j, is a function of the difference between the intrinsic atoms: Ii - Ij. The perturbation is diminished over distance; the functional dependence of the diminution is taken to be the square of the count of atoms in the shortest path between atoms i and j (rij). The perturbations are summed over the whole molecule:
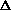 Ii =
Ii =  (Ii - Ij)/rij2
(Ii - Ij)/rij2
The electrotopological state, called the E-state, of atom i, Si, is given as the sum of the intrinsic state and the perturbations:
Si = Ii + 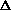 Ii
Ii
The E-state index values Si are output to the .S file if the appropriate records are selected and the .S file is selected in the Menu.
An example calculation of the contributions to the electrotopological state indices is given for alanine.
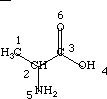
| I(1) = 2.000 | I(4) = 6.000 |
| I(2) = 1.333 | I(5) = 4.000 |
| I(3) = 1.667 | I(6) = 7.000 |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 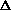 Ii = row sum Ii = row sum | |
| 1 | 0.0 | 0.1667 | 0.0370 | -0.2500 | -0.2222 | -0.3125 | -0.5810 | |
| 2 | -0.1667 | 0.0 | -0.0833 | -0.5185 | -0.6667 | -0.6296 | -2.0648 | |
| 3 | 0.0370 | 0.0833 | 0.0 | -1.0833 | -0.2593 | -1.3333 | -2.6296 | |
| 4 | 0.2500 | 0.5185 | 1.0833 | 0.0 | 0.1250 | -0.1111 | 1.8657 | |
| 5 | 0.2222 | 0.6667 | 0.2593 | -0.1250 | 0.0 | -0.1875 | 0.8356 | |
| 6 | 0.3125 | 0.6296 | 1.3333 | 0.1111 | 0.1875 | 0.0 | 2.5741 | |
| sum | 0.0000 | |||||||
| The summary of calculated E-State Values for Alanine: | 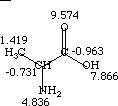 |
 Ii Ii |
The electrotopological state indices have been used in developing QSAR relations for a variety of biological properties in addition to certain physicochemical properties.
The method described in the previous section applies to the each skeletal atom (together with its attached hydrogen atoms). It is useful, however, to develop an E-state index for the hydrogen atoms alone. This is especially useful for hydrogen atoms which are described as polar. For this reason we have adopted the same formalism as given above but with a somewhat different approach for the intrinsic state value. We have taken I(H) to be primarily dependent upon the attached atom and have used the following expression:
I(H) = ( v -
v -  )2/
)2/
This expression gives rise to the values in the following table.
| X-H | X( v - v -  ) ) | I(H) |
| -OH | 4 | 16.0 |
| =NH | 3 | 9.0 |
| -NH2 | 2 | 4.0 |
| =CH | 2 | 4.0 |
| -NH- | 2 | 2.0 |
| =CH2 | 1 | 1.0 |
| =CH- | 1 | 1.0 |
| -CH< | 0 | 0.0 |
| -CH2- | 0 | 0.0 |
| -CH3 | 0 | 0.0 |
As an example of the hydrogen E-state index values, consider the following for 3,3-dimethyl-4,5-dichlorohexanol. Polar hydrgen atoms have very large positive values; less polar hyrogens have proportinally lsmaller values. Even hydrogen atoms located on carbon atoms near halogen atoms are shown to be influenced.
| Atom ID | Group | Valence Delta | HES, Si | Intrinsic State, Ii | Connected Atoms |
| 1 | CH3 | 1.00 | -1.382 | 0.000 | 2 |
| 2 | CH | 3.00 | 0.089 | 0.000 | 1 3 4 |
| 3 | Cl | 0.78 | 0.000 | 0.000 | 2 |
| 4 | CH | 3.00 | 0.073 | 0.000 | 2 5 6 |
| 5 | Cl | 0.78 | 0.000 | 0.000 | 4 |
| 6 | C | 4.00 | 0.000 | 0.000 | 4 7 8 9 |
| 7 | CH3 | 1.00 | -1.224 | 0.000 | 6 |
| 8 | CH3 | 1.00 | -1.224 | 0.000 | 6 |
| 9 | CH2 | 2.00 | -2.361 | 0.000 | 6 10 |
| 10 | CH2 | 2.00 | -4.374 | 0.000 | 9 11 |
| 11 | OH | 5.00 | 25.979 | 16.000 | 10 |
These values for I are used to compute an E-State index for each hydrogen atom in the molecule. These are stored in the .S file as HES.
The formalism for the hydrogen E-State is parallel to that for the E-State index of each atom (or
hydride group). For the hydrogen E-State the intrinsic state value is set to zero. The
perturbation term ( HIij) depends on the valence
state electronegativity of the hydride group as given by the Kier-Hall (relative)
electronegativity: RKHE = (
HIij) depends on the valence
state electronegativity of the hydride group as given by the Kier-Hall (relative)
electronegativity: RKHE = ( v -
v -
 )/n2 where n is the principal quantum number
of the valence electrons of the atom. For the hydrogen E-State the perturbation term,
)/n2 where n is the principal quantum number
of the valence electrons of the atom. For the hydrogen E-State the perturbation term,
 HIij = (RKHEi -
RKHEj)/rij2 in which rij is the number of atoms
in the shortest path between atoms i and j. In addition to the perturbation
contribution for every other hydride group, an additional contribution arises from the bond
between the hydrogen atom and the atom to which it is bonded. Thus, for the hydrogen E-State
value on atom i, HS(i) = (
HIij = (RKHEi -
RKHEj)/rij2 in which rij is the number of atoms
in the shortest path between atoms i and j. In addition to the perturbation
contribution for every other hydride group, an additional contribution arises from the bond
between the hydrogen atom and the atom to which it is bonded. Thus, for the hydrogen E-State
value on atom i, HS(i) = (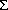 j
j
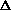 HIij + ((-0.2) - RKHEi). The
electronegativity of hydrogen is taken as -0.2 (on a scale in which C(sp3) is set
to zero). For simplicity of use the actual value computed by Molconn-Z is taken as the
negative of the value defined above to make all the values positive: HS(i) <-- -HS(i).
HIij + ((-0.2) - RKHEi). The
electronegativity of hydrogen is taken as -0.2 (on a scale in which C(sp3) is set
to zero). For simplicity of use the actual value computed by Molconn-Z is taken as the
negative of the value defined above to make all the values positive: HS(i) <-- -HS(i).
In the manner described here, Molconn-Z computes the hydrogen E-State values for each atom, a parallel set of values to the E-State values for each atom. The hydrogen E-State values are not highly correlated with the E-State values. The hydrogen E-State values are useful for characterizing both the polar and nonpolar portions of the structure. This new formalism repairs a bug in the earlier algorithm in which molecular symmetry was not always kept.
For data sets with a wide variety of atom types, it is useful to have E-state indices for each atom type. Molconn-Z computes the E-state for each skeletal atom (with attached hydrogens) and then sums the values for all the atoms of a given atom type. These atom type E-state indices are then output to the .S file for use in analysis.
Two papers have been written and a third submitted which discuss the development and use of the atom type E-state indices. In the first paper the definitions are given along with an application to the boiling point of alkanes and alcohols. In the second paper the atom type E-state indices are used to define a molecular similarity measure and as a basis for database searching. In the third paper atom type E-state indices are used to model the boiling point of a set of 372 alkanes, alcohols and chloroalkanes using artificial neural networks.
The following table shows the results of a sample computation for the molecule 3,3-dimethyl-4,5-dichlorohexanol. Part of the Molconn-Z output in the .L file is given here to show the E-state indices. Following that table is the table of atom type E-state indices.
| Atom ID | Group | Valence Delta | EState, Si | Intrinsic State, Ii | Connected Atoms |
| 1 | CH3 | 1.00 | 1.87336 | 2.000 | 2 |
| 2 | CH | 3.00 | -0.05721 | 1.333 | 1 3 4 |
| 3 | Cl | 0.78 | 5.83490 | 4.111 | 2 |
| 4 | CH | 3.00 | -0.08674 | 1.333 | 2 5 6 |
| 5 | Cl | 0.78 | 6.04310 | 4.111 | 4 |
| 6 | C | 4.00 | -0.08584 | 1.250 | 4 7 8 9 |
| 7 | CH3 | 1.00 | 2.01366 | 2.000 | 6 |
| 8 | CH3 | 1.00 | 2.01366 | 2.000 | 6 |
| 9 | CH2 | 2.00 | 0.69269 | 1.500 | 6 10 |
| 10 | CH2 | 2.00 | 0.16650 | 1.500 | 9 11 |
| 11 | OH | 5.00 | 8.73082 | 6.000 | 10 |
A simple set of symbols was developed for the atom type E-state. For the methyl groups the symbol is SsCH3. For methylene it is SssCH2; for the terminal double-bonded CH2, it is SdCH2 and for the keto oxygen, it is SdO. A set of the symbols is given in Appendix III, Section A. For the molecule given above, the atom type E-state indices are as follows:
| Atom Type | E-state Value |
| SsCH3 | 5.091 |
| SssCH2 | 0.860 |
| SsssCH | -0.087 |
| SssssC | -0.086 |
| SsOH | 8.731 |
| SsCl | 11.878 |
HCsats: Carbon sp3 bonded to other saturated carbon atoms
HCsatu: Carbon sp3 bonded to unsaturated carbon atoms
HdsCH: Carbon atoms in the vinyl group, =CH-
HdCH2: Carbon atoms in the terminal vinyl group, =CH2
Havin: Carbon atoms in the vinyl group, =CH-, bonded to an aromatic carbon
HaaCH: Carbon sp2 which are part of an aromatic system
All of the above descriptors are found in record #31 in the .S file. In addition there is a general descriptor for non-polar hydrogen atoms which is the sum of the Hydrogen E-State values for all non-polar C-H bonds, Hother, also found in record #31 in the .S file.
Descriptors that represent the potential for internal hydrogen bonding is determined as follows: There is a donor and an acceptor separated by n bonds along a path, the donor is characterized by the Hydrogen E-State value, the acceptor is characterized by the E-State value, and the internal hydrogen bond descriptor, SHBintn (where n is path length), is computed as the product of the Hydrogen E-State value times the E-State value. The most likely occurrence of internal hydrogen bonding is for paths of length 3 and 4. The complete hydrogen-bonded internal ring also includes the X-H bond as well as the hydrogen bond. Thus, the ring size is n + 2. Currently descriptors are computed for values of n from 2 to 10 although only those for n = 3, 4 are considered most useful. Also the count of the corresponding occurrences are included as nHBintn. See Appendix I for specific output location for these descriptors.
Iij = (Ii + Ij)/2
BESij = Iij + 
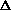 Iij/rij2
Iij/rij2
where rij is computed as the average rij for the atoms in the two bonds.
These computed values for individual bonds are then collected for each type of bond in the molecule. Appendix III lists the current set of bond types, numbering 895 at present.
The symbol for each bond type consists of an indicator for bond order, e1, e2, e3 or ea. The two atom types are encoded next. Finally, if necessary, an indication of unused bonds is given. For the bond between -CH3> and -CH2-, the symbol is e1C1C2. For the bond between =CH- and -CH2-, it is e1C2C2d. For the bond between =CH- and =CH-, there are two possibilities: e1C2C2d and e2C2C2s. The list of bond types and their symbols is given in Appendix III.
For the molecule 3,3-dimethyl-4,5-dichlorohexanol, the following tables of values are given in the Molconn-Z .L file.
*--> Bond E-State indices from bond types
Bond Atom IDs Atom Types Bond Type Bond Bond No. i j i j Order No. E-State Symbol ---- ---------- --------------- ----- ---- ------- ------ 1 1 2 -CH3 >CH- 1 69 1.383 e1C1C3 2 2 3 >CH- -Cl 1 290 3.734 e1C3Cl 3 2 4 >CH- >CH- 1 264 .389 e1C3C3 4 4 5 >CH- -Cl 1 290 3.973 e1C3Cl 5 4 6 >CH- >C< 1 268 .359 e1C3C4 6 6 7 >C< -CH3 1 73 1.491 e1C1C4 7 6 8 >C< -CH3 1 73 1.491 e1C1C4 8 6 9 >C< -CH2- 1 138 .728 e2C2C4 9 9 10 -CH2- -CH2- 1 132 .843 e1C2C2 10 10 11 -CH2- -OH 1 148 5.220 e1C2O1
*--> Bond Type Indices:
NET ETS Bond Type No. Bond Count Bond E-State Symbol --- ---------- ------------ --------- 69 1 1.38273 e1C1C3 73 2 2.98245 e1C1C4 132 1 .84259 e1C2C2 138 1 .72820 e2C2C4 148 1 5.21986 e1C2O1 264 1 .38944 e1C3C3 268 1 .35870 e1C3C4 290 2 7.70714 e1C3Cl
These indices have not yet been described in the literature. The bond type E-state indices are output to the .E file by Molconn-Z. Two catagories may be selected, inorganic or organic, in the Menu.
For molecular connectivity indices, when a data set consists of diverse molecular structures, the collinearity is usually not large enough to pose a significant problem. However, when the set of molecules covers a large range in molecular size and/or there is not a high degree of structure diversity, collinearity can become a problem in various forms of statistical analysis.
There are well known methods for introducing orthogonality into a set of variables. Principal component analysis (PCA) is often used. In this method, the set of variables, xi, is transformed by linear combinations into a new set, called xi'. The new variables are obtained as the eigenvectors of either the variance/covariance matrix or the correlation matrix of the original variables. In this rather straightforward manner, each new principal component is a linear combination of all the original xi variables. Such an arrangement facilitates subsequent statistical analysis but interpretation is obscured because each principal component is a linear combination of every variable in the data set.
A second method is to use a Gram-Schmidt type orthogonalization (GSO). For a set of variables (x, i=1,n), x1 is selected as the first new variable, x1'. x2' is created to be orthogonal to x1'. A simple way to obtain x' is to regress x2 against x1' (=x1). The set of residuals from this regression, res2, is set equal to x2'. Because res2 is that part of x2 which is not correlated to x1, that is, res2 (=x2') orthogonal to x1. One can proceed in this manner to create a set of orthogonal indices, xi'. This method is a bit more cumbersome than using principal components. The first two or three of these xi' indices may also have more interpretability than the principal components. However, ultimately, interpretability is largely lost. Further, in both of these methods, the set of orthogonal indices is dependent upon the specific data set from which they were generated. Adding a few new observations tends to diminish the orthogonality as well as the interpretation given to the orthogonal indices.
Another method which we have been using approaches the problem somewhat differently. A major aspect of the collinearity problem is the significant contribution of molecular size to the constitution of the chi indices. In fact, when the data set spans a large size range, the collinearity tends to increase significantly. For this reason, we have chosen to create a largely, but not exactly, orthogonal index which is largely independent of molecular size. After size is removed, the salient aspects of structure encoded in the chi indices remains. These important aspects - branching, cyclization, heteroatom content, heteroatom position - are emphasized in these new indices.
For each order of chi path index for a given molecule, we created an index to encode size only
for each order of path. This quantity is defined for the graph of the same size as the given
molecule but for the unbranched, acyclic graph: m N
for the simple path index and mcNv for the valence path index. The new, largely size-independent
chi index of order m is called the difference chi index. The difference chi
index is defined for both the simple path index and the valence path index of order m.
N
for the simple path index and mcNv for the valence path index. The new, largely size-independent
chi index of order m is called the difference chi index. The difference chi
index is defined for both the simple path index and the valence path index of order m.
dm N = m
N = m P
- m
P
- m N, for simple path indices
N, for simple path indices
dm Nv =
m
Nv =
m Pv -
m
Pv -
m Nv, for valence path indices
Nv, for valence path indices
In this manner, the size factor in the chi path index is subtracted out, leaving an index which is very nearly independent of size. For alkanes, the relation is exact. However, for heteroatom-containing indices, the relation is not exact. The size-independence of each difference index depends somewhat on the specific set of molecules. However, the definition of the difference chi index is independent of the data set. The difference chi indices are output to the .S file if it is selected in the Menu and if the appropriate records are selected for the .S file.
The difference chi indices are illustrated in the following table.
Graph 1N d1
1
N2 d1
v 3
N d3
P 3
Nv d3
Pv ------------ ---- ---- ----- ----- ---- ---- ---- -----
It is possible, then, to remove that part of each chi index which encodes only the sigma electrons and leave that part which encodes the pi and lone pair electrons. This process simply involves subtraction of the simple index from the corresponding valence index of the same order. These indices are called the delta chi indices and are defined as follows.
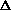 m
m t = m
t = m tv - m
tv - m t
t
where t stands for the types of chi indices: path (P), cluster (C), path-cluster (PC), and chain (CH).
The following table gives examples for the delta chi indices for four molecules and the
three indices:  1
1 t,
t,  3
3 P,
P,  4
4 PC.
PC.
Graph1
t
3
P
4
PC --------------- ----- ----- -----
The delta chi indices are not included in the .S output file. The user can easily produce the delta chi indices in the processing of the .S file in conjunction with the statistical analysis of the data set.
It should be pointed out that it is also possible to construct the sum of a simple chi index and its valence counterpart:
 m
m t = m
t = m tv + m
tv + m t
tA given sum chi index is, in general, orthogonal to the delta chi index of the same order. Thus, it is possible to reduce collinearity in the data set by converting from the chi indices to the set of delta and sum chi indices.
Petitjean also defined a graph shape index: I = (D - R)/D. This index characterizes the shape of various graphs. For any graph with all equivalent vertices, D = R and I = 0. Hence, a purely monocyclic graph has I = 0. For an acyclic graph, either D is even and D = 2R or D is odd and D = 2R - 1. For n-hexane R = 3 and D = 5 and I = 2/3; for n-heptane R = 3 and D = 6 and I = 3/6 = 1/2.
The vertex eccentricities are output to the .S file if it is selected in the Menu and if the appropriate records are selected for the .S file.
A major step towards this goal has been recently published. A target
property or activity value together with the QSAR equations based on chi and/or kappa indices yields target values
for 1 , 2
, 2 and
3
and
3 P indices. Using these low order molecular connectivity indices,
we have developed a formal scheme for conversion of the chi indices into path counts and subsequently
into counts of atoms types (vertex degrees). These atom types can be assembled directly into molecular
structures.
P indices. Using these low order molecular connectivity indices,
we have developed a formal scheme for conversion of the chi indices into path counts and subsequently
into counts of atoms types (vertex degrees). These atom types can be assembled directly into molecular
structures.
chi indices --> path counts --> vertex degrees (atom types) --> graphs
The initial papers in the series deal with the molecular skeletons using only the simple chi indices. Incorporation of heteroatoms and bonding schemes are added from the experience of the user and the nature of the data sets and the property of interest. Current work is aimed at a broader scheme which will include heteroatoms and their placement directly.
The equations which related the basic graph quantities have been derived in a rigorous manner. These relating equations contain path counts, vertex degree counts and the number of rings:
1D = - 4D + 2p - 1p + 3 -3R
2D = 34D - 22p + 31p - 3 +3R
3D = -34D + 2p - 1p + 1 -R
where iD is the number of vertices of degree i; ip is the number of paths of length i edges; and R is the number of rings in the graph. See references 1 and 2 below for the details of the process. From the set of vertex degrees, Faradzhev has shown that it is possible to construct all the graphs consistent with that set of vertex degrees. The references below give detailed examples of the overall scheme and each of each steps.
The inverse QSAR process is not part of the Molconn software. However, the necessary chi indices along with the path counts (nxpi) and vertex degree counts (ndi) are all computed by Molconn-Z. See Appendix I for the list of variables in the .S file.
For our purposes here we will give the overall formal scheme as illustrated by one simple example taken from our first paper on the inverse QSAR investigation.
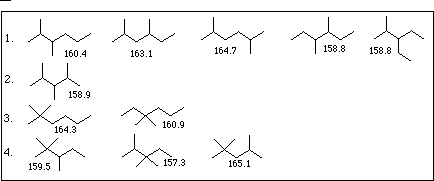
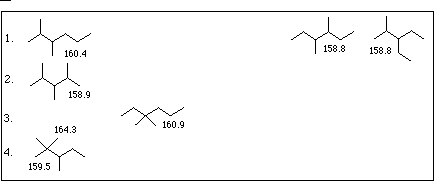
| QSAR Equations | Target Property Value | |
|---|---|---|
| a. | mv = 42.87 + 27.43 * 1 + 7.69 * 2 + 7.69 * 2 - 3.50 * 3 - 3.50 * 3 | mv = 158. to 162. |
| b. | mv = 44.40 + 25.49 * 1 + 7.49 * 2 + 7.49 * 2 - 0.058 * 4 - 0.058 * 4 P P | |
| c. | mv = 48.09 + 23.82 * 1 + 8.03 * 2 + 8.03 * 2 - 9.70 * 6 - 9.70 * 6 P P | |
| d. | mv = 40.50 + 35.72 * 1 - 4.64 * 3 - 4.64 * 3 P - 17.72 * 6 P - 17.72 * 6 P P | |
| e. | mv = 47.67 + 31.14 * 1 + 0.675 * 4 + 0.675 * 4 P - 7.22 * 6 P - 7.22 * 6 P P |
1 = 3.498 to 3.616
= 3.498 to 3.616
2 = 3.275 to 3.413
= 3.275 to 3.413
1p = 7, 2p = 8, 9, 10
A = 8, R = 0
| 1D | 2D | 3D | 4D | |
|---|---|---|---|---|
| 1. | 4 | 2 | 2 | 0 |
| 2. | 5 | 0 | 3 | 0 |
| 3. | 4 | 3 | 0 | 1 |
| 4. | 5 | 1 | 1 | 1 |